CS 학습 - 9월 3주차 | Paul’s Archives

알고리즘

Sort

1. 삽입 정렬 (Insertion Sort)

1-1. 개념

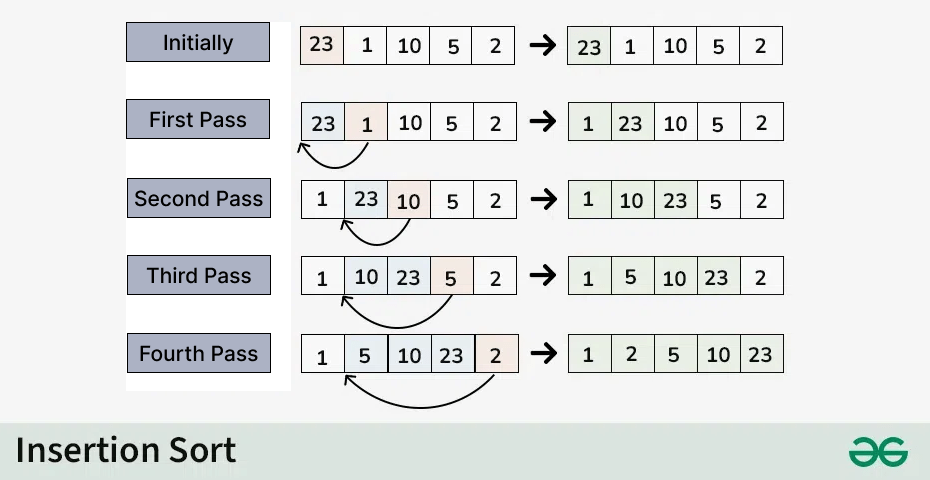
삽입 정렬은 처리되지 않은 데이터를 이미 정렬된 부분의 적절한 위치에 삽입해 나가는 방식으로 동작한다. 손안의 카드를 정렬할 때, 새로운 카드를 이미 정렬된 카드 뭉치의 올바른 자리에 꽂는 과정과 유사하다.

2번째 원소부터 시작하여 그 앞(왼쪽)의 데이터들과 비교하여 삽입할 위치를 지정하고, 데이터를 뒤로 옮긴 후 해당 자리에 삽입한다.

1-2. 시간 복잡도

최선(Best): $O(n)$ - 이미 데이터가 모두 정렬되어 있는 경우, 외부 루프만 한 번 순회한다.
평균(Average): $O(n^2)$
최악(Worst): $O(n^2)$ - 데이터가 역순으로 정렬되어 있는 경우, 모든 요소를 비교하고 이동시켜야 한다.

알아두면 좋은 팁 삽입 정렬은 데이터셋의 크기가 작거나, 데이터가 거의 정렬된 상태일 때 매우 효율적으로 동작한다. 이런 특성 때문에 다른 복잡한 정렬 알고리즘(예: 팀 정렬)의 일부로 사용되기도 한다.

1-3. Python 구현 코드

def insertion_sort(arr):
    # 배열의 2번째 요소(인덱스 1)부터 시작
    for i in range(1, len(arr)):
        key = arr[i]  # 정렬할 대상이 되는 요소
        j = i - 1     # 비교 대상이 되는 정렬된 부분의 마지막 인덱스
        
        # key를 정렬된 부분의 올바른 위치에 삽입
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j] # 요소를 한 칸씩 오른쪽으로 이동
            j -= 1
        arr[j + 1] = key # 찾은 위치에 key를 삽입
    return arr

# 예시
data = [5, 2, 4, 6, 1, 3]
print(f"삽입 정렬 결과: {insertion_sort(data)}")

2. 버블 정렬 (Bubble Sort)

2-1. 개념

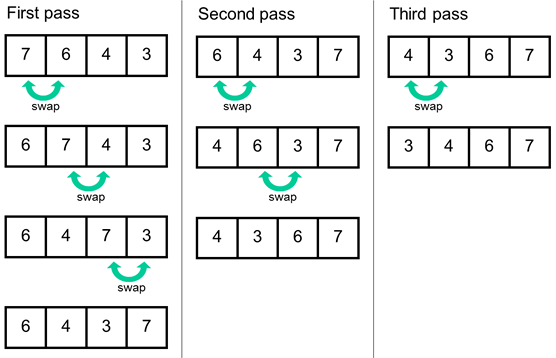
버블 정렬은 인접한 두 개의 원소를 비교하며 자리를 교환하는 방식으로 동작한다. 배열의 처음부터 끝까지 순회하면서, 왼쪽 값이 오른쪽 값보다 크면 두 값의 위치를 바꾼다. 이

러한 한 번의 순회(Pass)가 끝나면 가장 큰 원소가 배열의 맨 끝으로 이동하게 된다. 이 과정을 배열의 크기만큼 반복한다. 마치 물속의 거품(Bubble)이 위로 올라오는 모습과 같아 버블 정렬이라는 이름이 붙었다.

2-2. 시간 복잡도

최선(Best): $O(n)$ - 이미 데이터가 정렬된 상태에서, 한 번의 순회 중 교환(swap)이 발생하지 않으면 정렬을 종료하는 로직을 추가했을 경우이다.
평균(Average): $O(n^2)$
최악(Worst): $O(n^2)$ - 데이터가 역순으로 정렬되어 있는 경우이다.

알아두면 좋은 팁 버블 정렬은 구현이 매우 간단하여 정렬 알고리즘의 기본 원리를 학습하는 데는 좋지만, 성능이 좋지 않아 실제 현업에서 사용되는 경우는 거의 없다.

2-3. Python 구현 코드

def bubble_sort(arr):
    n = len(arr)
    # 배열의 크기만큼 외부 루프를 반복
    for i in range(n):
        swapped = False
        # 이미 정렬된 마지막 요소들을 제외하고 내부 루프를 반복
        for j in range(0, n - i - 1):
            # 왼쪽 요소가 오른쪽 요소보다 크면 교환
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                swapped = True
        # 한 번의 순회 동안 교환이 일어나지 않았다면, 이미 정렬된 상태
        if not swapped:
            break
    return arr

# 예시
data = [5, 2, 4, 6, 1, 3]
print(f"버블 정렬 결과: {bubble_sort(data)}")

3. 병합 정렬 (Merge Sort)

3-1. 개념

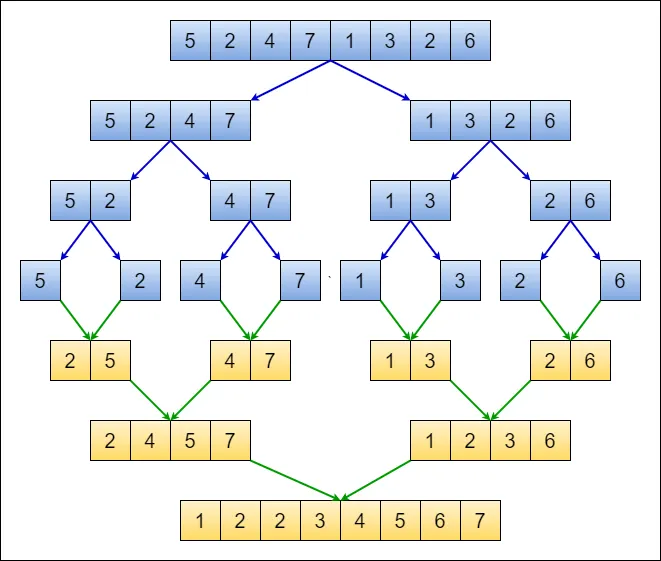
병합 정렬은 분할 정복(Divide and Conquer) 패러다임을 사용하는 대표적인 정렬 알고리즘이다.

분할(Divide): 배열의 크기가 1이 될 때까지 재귀적으로 계속해서 반으로 나눈다.
정복(Conquer): 나누어진 작은 배열들을 2개씩 쌍을 이루어 정렬하면서 병합(Merge)한다. 이 과정을 모든 배열이 다시 하나로 합쳐질 때까지 반복한다.

3-2. 시간 복잡도

최선(Best): $O(n \log n)$
평균(Average): $O(n \log n)$
최악(Worst): $O(n \log n)$

알아두면 좋은 팁 병합 정렬은 데이터의 분포와 상관없이 항상 $O(n \log n)$의 시간 복잡도를 보장하여 안정적(Stable)이다. 하지만 정렬 과정에서 임시 배열을 위한 추가적인 메모리 공간($O(n)$) 이 필요하다는 단점이 있다.

3-3. Python 구현 코드

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    
    # 1. 분할 (Divide)
    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])
    right_half = merge_sort(arr[mid:])
    
    # 2. 정복 및 병합 (Conquer and Merge)
    merged_arr = []
    l_idx, r_idx = 0, 0
    while l_idx < len(left_half) and r_idx < len(right_half):
        if left_half[l_idx] < right_half[r_idx]:
            merged_arr.append(left_half[l_idx])
            l_idx += 1
        else:
            merged_arr.append(right_half[r_idx])
            r_idx += 1
            
    # 남은 요소들을 추가
    merged_arr.extend(left_half[l_idx:])
    merged_arr.extend(right_half[r_idx:])
    
    return merged_arr

# 예시
data = [5, 2, 4, 6, 1, 3]
print(f"병합 정렬 결과: {merge_sort(data)}")

4. 힙 정렬 (Heap Sort)

4-1. 개념

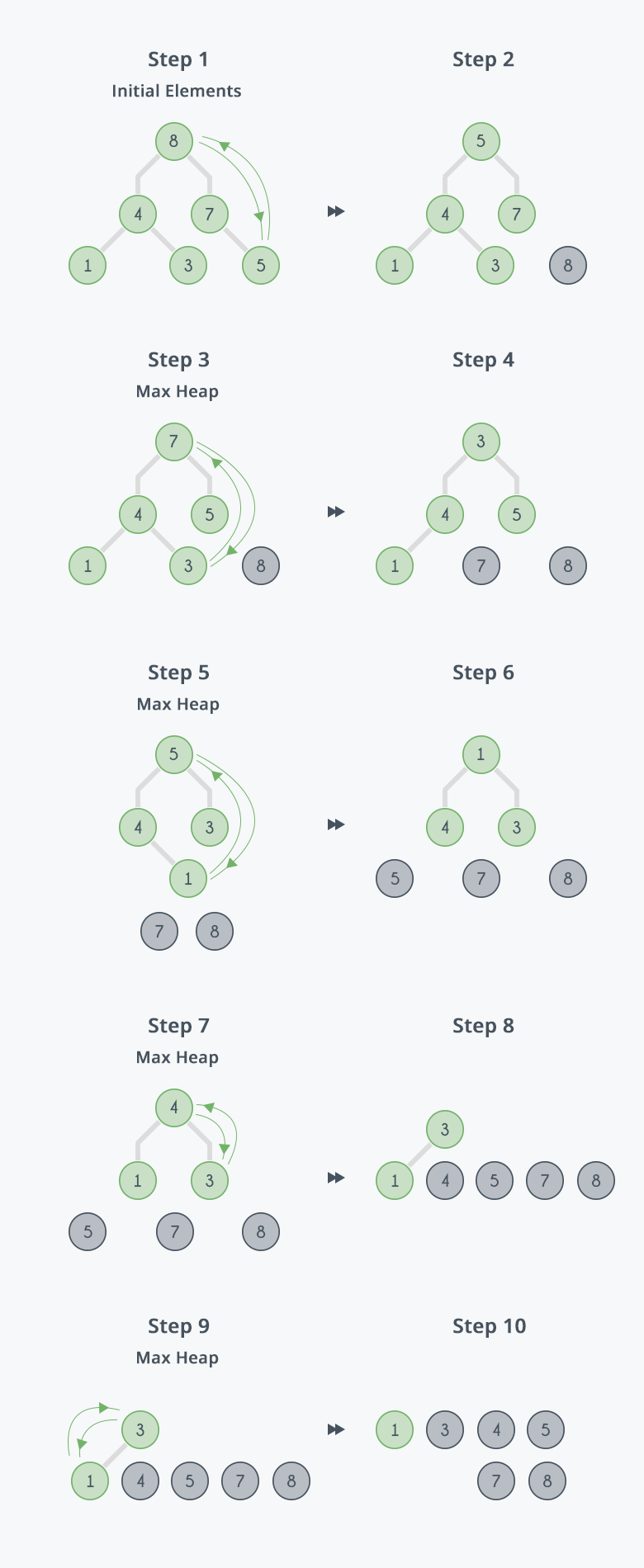
힙 정렬은 힙(Heap) 자료구조를 이용하여 정렬하는 알고리즘이다. 힙은 ‘완전 이진 트리’의 한 종류로, 부모 노드의 값이 항상 자식 노드의 값보다 크거나 같은(최대 힙) 또는 작거나 같은(최소 힙) 속성을 만족한다.

주어진 데이터를 최대 힙(Max Heap) 구조로 만든다.
힙에서 가장 큰 값은 루트(root) 노드에 위치한다. 이 루트 노드를 배열의 가장 마지막 요소와 바꾼다.
힙의 크기를 하나 줄이고, 다시 힙 속성을 만족하도록 구조를 재조정(heapify)한다.
힙의 크기가 1이 될 때까지 2~3번 과정을 반복한다.

4-2. 시간 복잡도

최선(Best): $O(n \log n)$
평균(Average): $O(n \log n)$
최악(Worst): $O(n \log n)$

알아두면 좋은 팁 힙 정렬은 병합 정렬과 달리 추가적인 메모리 공간을 거의 사용하지 않는($O(1)$) 장점이 있으며, 항상 $O(n \log n)$의 성능을 보장한다. 우선순위 큐를 구현할 때 매우 유용하다.

4-3. Python 구현 코드

def heapify(arr, n, i):
    largest = i  # 현재 서브트리의 루트
    left = 2 * i + 1
    right = 2 * i + 2
    
    # 왼쪽 자식이 루트보다 크면 largest를 업데이트
    if left < n and arr[i] < arr[left]:
        largest = left
        
    # 오른쪽 자식이 largest보다 크면 largest를 업데이트
    if right < n and arr[largest] < arr[right]:
        largest = right
        
    # largest가 변경되었다면, 루트와 교환하고 재귀적으로 heapify 호출
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)
    
    # 1. 최대 힙(Max Heap) 구성
    # 마지막 비단말 노드부터 시작하여 루트까지 heapify 수행
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)
        
    # 2. 힙에서 요소를 하나씩 추출하여 정렬
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # 루트(최댓값)를 배열의 끝으로 이동
        heapify(arr, i, 0) # 크기가 줄어든 힙에 대해 heapify 수행
        
    return arr

# 예시
data = [5, 2, 4, 6, 1, 3]
print(f"힙 정렬 결과: {heap_sort(data)}")

4-4. heapq 모듈 사용 예시 및 장단점

Python의 내장 라이브러리인 heapq를 사용하면 힙 자료구조를 간단하게 활용할 수 있다. 다음은 heapq를 이용해 리스트를 정렬하는 예시 코드이다.

import heapq

def heapq_sort(arr):
    heap = []
    # 모든 원소를 힙에 차례대로 삽입
    for num in arr:
        heapq.heappush(heap, num)
    
    # 힙에서 모든 원소를 차례대로 꺼내 정렬된 리스트 생성
    sorted_arr = []
    while heap:
        sorted_arr.append(heapq.heappop(heap))
        
    return sorted_arr

# 예시
data = [5, 2, 4, 6, 1, 3]
print(f"heapq를 이용한 정렬 결과: {heapq_sort(data)}")

# 더 간결한 방법: heapify 사용
def heapq_sort_concise(arr):
    # 리스트를 한 번에 힙으로 변환 (O(n))
    heapq.heapify(arr)
    
    sorted_arr = []
    while arr:
        sorted_arr.append(heapq.heappop(arr))
        
    return sorted_arr

import heapq

# 최대 힙으로 사용할 리스트
max_heap = []
data = [3, 5, 1, 9, 4, 8]

# 1. 최대 힙에 원소 추가 (부호를 바꿔서 heappush)
print("--- 최대 힙에 원소 추가 ---")
for num in data:
    heapq.heappush(max_heap, -num)
    print(f"{num} 추가 후 힙 상태: {max_heap}")

print("\n최종 최대 힙 (내부 표현):", max_heap) # 내부적으로는 음수 값을 가진 최소 힙
print(f"가장 큰 값(루트): {-max_heap[0]}")

print("\n--- 최대 힙에서 원소 추출 ---")
# 2. 최대 힙에서 원소 추출 (heappop 후 부호를 다시 변경)
while max_heap:
    # 가장 작은 음수(원래는 가장 큰 양수)를 꺼내서 부호를 복원
    max_val = -heapq.heappop(max_heap)
    print(f"추출된 최댓값: {max_val}")

알아두면 좋은 팁 기존 리스트를 제자리에서 힙으로 변환하는 heapq.heapify(list) 함수를 사용하면 $O(n)$의 시간 복잡도로 힙을 구성할 수 있어, 모든 원소를 하나씩 heappush 하는 것보다 효율적이다.

구현 대비 장점
- 간결성: 복잡한 heapify 로직을 직접 구현할 필요 없이, 몇 줄의 코드로 힙 기능을 사용할 수 있어 매우 편리하다.
- 성능: 내장 모듈은 C언어로 구현되어 있어 일반적으로 직접 Python으로 구현한 코드보다 실행 속도가 빠르다.
- 안정성: 이미 충분히 검증된 라이브러리이므로 직접 구현 시 발생할 수 있는 실수를 방지하고 코드의 안정성을 높일 수 있다.
구현 대비 단점
- 추상화: 내부 동작 원리가 감춰져 있어 힙 정렬의 학습 목적으로는 적합하지 않다.
- 추가 메모리 사용: 위 예시처럼 정렬된 결과를 담을 새로운 리스트가 필요하므로, 제자리 정렬(in-place sort)이 아니며 $O(n)$의 추가 공간이 필요하다.
- 최소 힙 고정: heapq는 최소 힙(Min Heap)만 지원하므로 최대 힙(Max Heap)이 필요할 경우, 값의 부호를 변경하는 등의 추가적인 처리가 필요하다.

— 2025년 9월 15일 학습

5. 퀵 정렬 (Quick Sort)

5-1. 개념

퀵 정렬 또한 분할 정복 패러다임을 사용하며, 평균적으로 매우 빠른 성능을 자랑한다.

배열 내에서 임의의 기준점, **피벗(Pivot)**을 선택한다.
피벗을 기준으로 피벗보다 작은 요소들은 왼쪽, 큰 요소들은 오른쪽으로 분할(Partition)한다.
분할된 양쪽의 부분 배열에 대해 재귀적으로 퀵 정렬을 수행한다.
부분 배열의 크기가 1 이하가 되면 정렬을 멈춘다.

5-2. 시간 복잡도

최선(Best): $O(n \log n)$ - 피벗이 항상 배열을 절반으로 분할할 때이다.
평균(Average): $O(n \log n)$
최악(Worst): $O(n^2)$ - 피벗이 항상 가장 작거나 가장 큰 값으로 선택되어 배열이 한쪽으로 치우치게 분할될 때이다 (예: 이미 정렬된 배열에서 항상 첫 요소를 피벗으로 선택).

알아두면 좋은 팁 퀵 정렬은 평균적인 성능이 매우 뛰어나 ‘퀵’이라는 이름이 붙었으며, 많은 프로그래밍 언어의 표준 정렬 라이브러리에서 기본 알고리즘으로 채택되곤 한다. 최악의 경우를 피하기 위해 피벗을 랜덤하게 선택하거나, 세 값의 중앙값(Median-of-three)을 선택하는 등의 기법이 사용된다.

5-3. Python 구현 코드

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    
    pivot = arr[len(arr) // 2] # 중앙값을 피벗으로 설정
    lesser_arr, equal_arr, greater_arr = [], [], []
    
    for num in arr:
        if num < pivot:
            lesser_arr.append(num)
        elif num > pivot:
            greater_arr.append(num)
        else:
            equal_arr.append(num)
            
    return quick_sort(lesser_arr) + equal_arr + quick_sort(greater_arr)

# 예시
data = [5, 2, 4, 6, 1, 3]
print(f"퀵 정렬 결과: {quick_sort(data)}")

6. 각 정렬 알고리즘 시간 복잡도 비교

알고리즘 (Algorithm)	최선 (Best)	평균 (Average)	최악 (Worst)
삽입 정렬	$O(n)$	$O(n^2)$	$O(n^2)$
버블 정렬	$O(n)$	$O(n^2)$	$O(n^2)$
병합 정렬	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$
힙 정렬	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$
퀵 정렬	$O(n \log n)$	$O(n \log n)$	$O(n^2)$

7. (번외) 그 외에 개발 시 사용하면 좋을 정렬 기법

이론적인 학습을 넘어 실제 개발 환경에서는 언어 차원에서 제공하는 내장 정렬 함수를 사용하는 것이 일반적이다. 이 함수들은 대부분의 상황에 최적화된 고성능 알고리즘을 사용한다.

팀 정렬 (Timsort)
- 개념: 병합 정렬과 삽입 정렬을 결합한 하이브리드 안정 정렬(Stable Sort) 알고리즘이다.
- 특징: 실제 데이터는 완전히 무작위가 아니라 어느 정도 정렬된 연속적인 부분(run)을 포함하는 경우가 많다는 점에서 착안되었다. 이런 ‘run’들을 찾아서 삽입 정렬로 처리하고, 이 run들을 효율적으로 병합해 나간다. 적응형(Adaptive) 알고리즘으로, 데이터의 상태에 따라 최적의 성능을 낸다.
- 용도: Python의 내장 정렬 함수(sorted(), list.sort())와 Java의 Arrays.sort() (객체 배열용)에서 표준 알고리즘으로 사용된다.
기수 정렬 (Radix Sort)
- 개념: 비교 기반 정렬이 아니다. 데이터의 자릿수(radix)를 이용하여 낮은 자릿수부터 정렬해 나가는 방식이다. 예를 들어, 10진수 정수를 정렬한다면 1의 자리, 10의 자리, 100의 자리 순으로 정렬을 수행한다.
- 특징: 시간 복잡도는 $O(d(n+k))$ (d: 자릿수, n: 데이터 개수, k: 기수)로, 데이터의 길이가 짧고 개수가 많을 때 비교 기반 정렬인 $O(n \log n)$보다 빠를 수 있다.
- 용도: 정수나 문자열 등 자릿수 구분이 명확한 데이터들을 정렬할 때 효과적이다. (예: 대규모 숫자 데이터 정렬, 사전순 문자열 정렬)
계수 정렬 (Counting Sort)
- 개념: 비교 기반 정렬이 아니다. 각 숫자가 몇 번 등장했는지 개수를 센 다음, 누적합을 이용하여 각 숫자의 정렬된 위치를 계산하는 방식이다.
- 특징: 데이터 값의 범위(range)가 데이터의 개수(n)에 비해 작을 때 매우 빠른 성능을 보인다. 시간 복잡도는 $O(n+k)$ (k: 데이터의 최댓값)이다.
- 용도: 정수 데이터, 특히 양수이고 값의 범위가 한정적일 때 사용하기 좋다. (예: 0~100점 사이의 시험 점수 정렬)

CS 학습 - 9월 3주차

CS 심화 스터디, 백엔드 도메인을 치밀하게 만들어보자