Introduction
본 포스트는 알고리즘 학습에 대한 정리를 재대로 하기 위하여 남기는 것입니다. 더불어 기본 내용은 나동빈 저의 〖이것이 취업을 위한 코딩 테스트다〗라는 교재 및 유튜브 강의의 내용에서 발췌했고, 그 외 추가적인 궁금 사항들을 검색 및 정리해둔 것입니다.
덧
중간에 뻬먹어서 재 포스팅합니다 ㅎㅎ!
퀵정렬
개념
- 기준 데이터를 설정하고, 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법입니다.
- 일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나입니다.
- 병합정렬과 더불어 프로그래밍 언어 정렬 라이브러리의 근간이 되는 알고리즘입니다.
- 가장 기본적인 퀵 정렬은 **첫 번째 데이터를 기준 데이터(Pivot)**으로 설정합니다.
퀵 정렬 동작 예시
- Step 0
피봇 값은 5, 왼쪽 부터 큰 데이터를 선택하므로 7이 되고 오른쪽부터 5보다 작은 값을 선택하므로 두 데이터 위치를 서로 변경합니다.
| pivot |
➡︎ |
|
|
|
|
|
|
⬅︎ |
|
5 |
7 |
9 |
0 |
3 |
1 |
6 |
2 |
4 |
8 |
- Step 1
피봇 값은 5, 4와 7을 바꾸고 왼쪽에선 다시 5보다 큰 값, 오른쪽에선 피봇보다 작은 값을 찾은 뒤 서로 위치를 바꿔줍니다.
| pivot |
|
➡︎ |
|
|
|
|
⬅︎ |
|
|
5 |
4 |
9 |
0 |
3 |
1 |
6 |
2 |
7 |
8 |
- Step 2
피봇 값은 5, 동일한 방식으로 진행하다가, 왼쪽에서 진행하던 값이 6을, 오른쪽으로 진행하던 값이 1을 지정하게 되어, 위치가 엇갈리는 경우 ‘피벗’과 작은 데이터’의 위치를 서로 변경합니다.
| pivot |
|
|
|
|
⬅︎ |
➡︎ |
|
|
|
5 |
4 |
2 |
0 |
3 |
1 |
6 |
9 |
7 |
8 |
- 분할 완료
이제 5의 왼쪽엔 5보다 작은 데이터가, 오른쪽엔 5보다 큰 데이터로 분할 됩니다. 이렇게 피벗을 기준으로 데이터 묶음을 나누는 작업을
분할(Devide, Partition) 라고 합니다.
| 5 |
보 |
다 |
작 |
음 |
⬇︎ |
5 |
보 |
다 |
큼 |
| 1 |
4 |
2 |
0 |
3 |
5 |
6 |
9 |
7 |
8 |
- 왼쪽 데이터 묶음 정렬
왼쪽에 있는 데이터에 대해서 마찬가지 방식으로 정렬(분할)을 진행합니다.
| pivot |
➡︎ |
|
⬅︎ |
|
|
|
|
|
|
1 |
4 |
2 |
0 |
3 |
5 |
6 |
9 |
7 |
8 |
- 오른쪽 데이터 묶음 정렬
마찬가지로 따로 데이터 정렬(분할)을 진행합니다.
|
|
|
|
|
|
pivot |
|
|
|
|
|
|
|
|
|
⬅︎ |
➡︎ |
|
|
| 1 |
4 |
2 |
0 |
3 |
5 |
6 |
9 |
7 |
8 |
- 여기서 중요한 점은 해당 방식으로 더 이상 분할 가능한 수준까지 계속 정렬을 진행하는, 재귀적인 방식의 정렬을 수행한다고 보시면 됩니다.
퀵 정렬이 빠른 이유 : 직관적인 이해
- 이상적인 경우 분할이 절반씩 일어난다면 전체 연산 횟수로 O(NlogN)을 기대할 수 있습니다.
- 너비 × 높이 = 𝑁 × 𝑙𝑜𝘨𝑁 = 𝑁𝑙𝑜𝘨𝑁
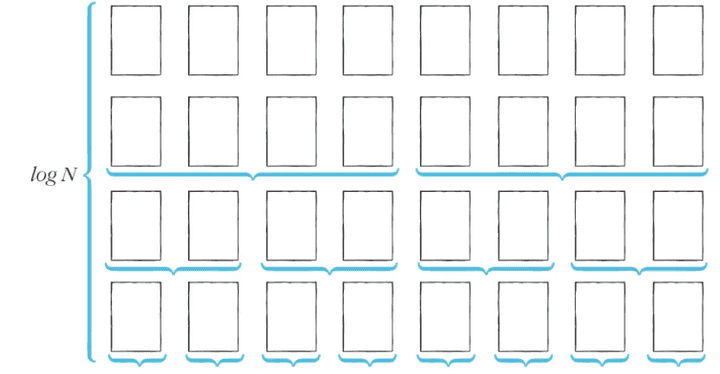점점 내려갈 수록 연산 횟수가 %2가 되고, 데이터 개수 N이기 때문에 시간복잡도가 빨라진다.
퀵 정렬의 시간 복잡도
- 퀵 정렬의 경우 O(𝑁𝑙𝑜𝘨𝑁)의 시간 복잡도를 가집니다.
- 최악의 경우 O(𝑁²)의 시간 복잡도를 가집니다. : 한 쪽 방향으로 편향된 분할이 발생 시
- 첫 번째 원소를 피봇으로 삼아 진행 시 이미 정렬된 배열에서 퀵 정렬을 수행시 발생됩니다.
| pivot |
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
퀵 정렬 소스코드 : 일반적인 방식(Python)
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array, start, end):
if (start >= end):
return
pivot = start
left = start + 1
right = end
while(left <= right):
while(left <= end and array[left] <= array[pivot]):
left += 1
while(right > start and array[right] >= array[pivot]):
right -=1
if (left > right):
array[right], array[pivot] = array[pivot], array[right]
else:
array[left], array[right] = array[right], array[left]
print(array)
quick_sort(array, start, right - 1)
quick_sort(array, right + 1, end)
quick_sort(array, 0, len(array) - 1)
print(array)
퀵 정렬 소스 코드 : 일반적인 방식(C++)
#include <bits/stdc++.h>
using namespace std;
int n = 10;
int target[10] = {5, 7, 9, 0, 3, 1, 6, 2, 4, 8}
void quickSort(int *target, int start, int end)
{
if (start >= end)
return ;
int pivot = start;
int left = start + 1;
int right = end;
while (left <= right)
{
while(left <= end && target[left] <= target[pivot])
left++;
while(right > start && target[right] >= target[pivot])
right--;
if (left > right)
swap(target[pivot], target[right]);
else
swap(target[left], target[right]);
}
quickSort(target, start, right - 1);
quickSort(target, right + 1, end);
}
int main(void)
{
quickSort(target, 0, n - 1);
for (int i = 0; i < n; i++)
cout << target[i] << ' ';
return (0);
}
퀵 정렬 소스코드 : 파이썬의 장점을 살린 방식
- list comprehension 기법을 활용해서 굉장히 간단하게 구현한 퀵 소트 입니다.
- 파이썬에 대해 여전히 연구가 필요한데, 상당히 간결한게 눈에 보입니다.(문제는 사용자인 내가 아직 확 와닻지 않는다는 거 😂)
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array):
if len(array) <= 1 :
return array
pivot = array[0]
tail = array[1:]
left_side = [x for x in tail if x <= pivot]
right_side = [x for x in tail if x > pivot]
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
print(quick_sort(array))
🧑🏻💻 알고리즘 박살내기 시리즈🧑🏻💻