신입 개발자 인터뷰 대비 : 2. 알고리즘

알고리즘

• 시간 복잡도 O(N^2)의 정렬 알고리즘과 O(NlogN)의 정렬 알고리즘을 직무 언어로 모듈 없이 구현할수 있는가?
  • 기본적으로 시간 복잡도 N^2, NlogN인 정렬 알고리즘은 각각 버블 정렬 알고리즘, 퀵 정렬 알고리즘이다.
  • 버블 정렬은 각 순회에서 가장 큰 요소를 배열 끝으로 이동시키는 방식으로 동작하고, 인접 요소를 계속 비교 및 스왑한다.
  • 퀵 정렬은 분할 정복 전략을 사용하여 배열을 정렬한다. 기준점(피봇)을 선택하고 이 기준점 대비 작은 요소와 큰 요소를 좌우로 분할하고 각 부분을 재귀적으로 정렬한다. - 버블 정렬 구현

    	public class BubleSort {
    		void bubleSort(int arr[]) {
    			int n = arr.length;
    			// 핵심적인 N^2 의 시간 복잡도는 이중 루프에서 발생한다. 
    			for (int i = 0; i < n - 1; i++) {
    				for (int j = 0; j < n - 1; j++) {
    					if (arr[j] > arr[j + 1]) {
    						int temp = arr[j];
    						arr[j] = arr[j+1];
    						arr[j+1] = temp;
    					}
    				}
    			}
    		}
    
    		void printArray(int arr[]) {
    			for (int i = 0; i < arr.length; i++)
    				System.out.print(arr[i] + " ");
    			System.out.println();
    		}
    
    		public static void main(String args[]) {
    			BubleSort ob = new BubbleSort();
    			int arr[] = {64, 34, 25, 12, 22, 11, 90};
    			ob.bubbleSort(arr);
    			System.out.println("Sorted array");
    			ob.printArray(arr);
    		}
    	}

  • 퀵 정렬 구현

    	  public class QuickSort {
    		  int partition(int arr[], int low, int high) {
    			  int pivot = arr[high];
    			  int i = low - 1;
    			  for (int j = low; j < high; j++) {
    				  if (arr[j] <= pivot) {
    					  i++;
    					  int temp = arr[i];
    					  arr[i] = arr[j];
    					  arr[j] = temp;
    				  }
    			  }
    			  int temp = arr[i+1];
    			  arr[i + 1] = arr[high];
    			  arr[high] = temp;
    			  
    			  return i + 1;
    		  }
    		  
    		  void sort(int arr[], int low, int high) {
    			  if (low < high) {
    				  int pi = partition(arr, low, high);
    				  sort(arr, low, pi - 1);
    				  sort(arr, pi + 1, high);
    			  }
    		  }
    		  
    		  static void printArray(int arr[]) {
    			int n = arr.length;
    			for (int i = 0; i < n; ++i)
    				System.out.print(arr[i] + " ");
    			System.out.println();
    		  }
    		  
    		  public static void main(String args[]) {
    			  int arr[] = {10, 7, 8, 9, 1, 5};
    			  int n = arr.length;
    			  
    			  QuickSort ob = new QuickSort();
    			  ob.sort(arr, 0, n - 1);
    			  
    			  System.out.println("sorted array");
    			  printArray(arr);
    		  }
    	  }

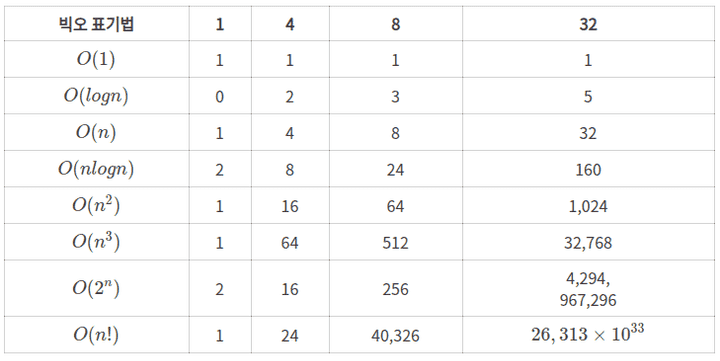
• 각 정렬 알고리즘의 Best와 Worst case 시간복잡도에 대해 알고, 각 특성을 설명할 수 있다.
  • 버블 정렬
    • 특성 :
      • 매우 직관적이고 간단한 정렬 방법
      • 인접한 두 원소 사이 검사를 통해 정렬을 진행하며, 정렬된 데이터를 다시 정렬 시 효과적이라는 장점이 있다.
      • 그러나 대부분의 경우 다른 정렬에 비해 비효율적이다.
    • Best Case 시간복잡도 : O(N)
      • 이미 정렬되어 있을 때, 버블 정렬은 최고의 속도를 낸다.
      • 이 때는 내부 루프에서 스왑이 일어나지 않으므로, 각 요소는 한 번씩만 확인하면 되기 때문이다.
      • 이때 중요한 것은 단순히 숫자 변화가 되어 있다! 가 아니라 정확하게 flag를 통해 변화 여부를 파악하는 기믹을 넣었을 때에 해당한다.

      public class OptimizedBubbleSort {
      	void bubbleSort(int arr[]) {
      		int n = arr.length;
      		boolean swapped;
      		for (int i = 0; i < n - 1; i++) {
      			swapped = false;
      			for (int j = 0; j < n - i - 1; j++) {
      				if (arr[j] > arr[j + 1]) {
      					int temp = arr[j];
      					arr[j] = arr[j + 1];
      					arr[j + 1] = temp;
      					swapped = true; // swap 발생 시 플래그 설정
      				}
      			}
      			// 한번 패스에서 스왑이 없었다면, 배열은 이미 정렬 된거
      			if (!swapped)
      				break;
      		}
      	}
      	
      	// 나머지 부분은 기존의 버블 정렬과 동일하게 가져가도 된다. 
      }

    • Worst Case 시간복잡도 : O(N^2)
      • 배열이 역순으로 정렬된 경우 최악의 시간복잡도를 보여준다.
      • 각 요소가 다음 요소와 무조건 비교 및 스왑을 해야하기 때문이다.
  • 퀵정렬
    • 특성
      • 분할 정복 전략을 사용하는 만큼, 높은 효율의 정렬 알고리즘이다.
      • 전반적인 면에서 빠른 속도를 유지하고, 대규모 데이터 셋에서도 효과적이다.
      • 하지만 피벗의 선택에 따라 성능이 크게 달라지고, 최악의 케이스도 생긴다는 점을 이해하고 있어야 한다.
    • Best Case 시간복잡도 : O(NlogN)
      • 퀵 정렬은 각 분할이 균등하게 이루어진 경우에 효과적이다.
      • 매번 피벗이 중앙값 근처로 선택되어 전체 배열을 균등하게 두 부분으로 나눌 때 최적의 성능을 보인다.
    • Worst Case 시간복잡도 : O(N^2)
      • 피벗이 최솟값이나 최댓값으로 선택될 때 발생한다. 이러한 경우 분할 과정이 한 쪽에 치우쳐지고, 모든 요소를 바꿔야 하므로, 최악의 시간복잡도를 야기한다.
  • 선택 정렬
    • 특성
      • 배열 전체의 가장 작은 요소를 찾아서 맨 앞으로 이동 시키고, 그 다음으로 작은 요소를 찾는 방식으로 정렬을 진행한다.
      • 매우 직관적이며, 추가적인 메모리가 복잡하게 필요하지 않다.
      • 그러나 대용량 데이터 양이 많아 질 수록 성능의 급격한 하락이 발생한다.
    • Best Case 시간복잡도 : O(N^2)
      • 입력 데이터의 정렬 상태와 무관하게 항상 모든 요소를 검사, 최선, 평균, 최악 모두 동일한 시간복잡도를 가진다.
    • Worst Case 시간복잡도 : O(N^2)
      • 입력 데이터의 정렬 상태와 무관하게 항상 모든 요소를 검사, 최선, 평균, 최악 모두 동일한 시간복잡도를 가진다.
  • 삽입 정렬
    • 특성
      • 각 반복에서 하나의 입력 요소를 적절한 위치에 삽입하여, 배열을 부분적으로 정렬한다.
      • 작은 데이터의 세트나 정령이 어느 정도 된 데이터에 대해서 빠르고, 안정적이게 정렬한다.
    • Best Case 시간복잡도 : O(N)
      • 배열이 이미 정렬 되어 있을 때, 전체 배열을
    • Worst Case 시간복잡도 : O(N^2)
      • 배열이 역순으로 정렬되어 있어서, 각 요소를 배열의 처음부터 그 위치까지 이동시켜야 하여서 최악의 케이스이다.
  • 병합 정렬
    • 특성
      • 분할정복알고리즘을 사용하여 배열을 절반으로 나누고, 각 부분을 재귀적으로 정렬하고 다시 병합하는 구조를 가진다.
      • 대규모 데이터 셋에 효과적이며, 안정적이다.
      • 그러나 이러한 구조가 추가적인 메모리를 필요로 한다.
    • Best Case 시간복잡도 : O(NlogN)
      • 배열을 분할하고 각 부분을 분할 및 병합하는데 필요한 로그 스케일의 단계를 거치다보니 일정한 시간복잡도를 요한다 .
    • Worst Case 시간복잡도 : O(NlogN)
      • 병합 정렬은 배열 초기 상태와 무관하게, Best와 동일하게 분할 및 병합 과정에서 필요한 시간으로 로그 스케일이 필요로 한다.
  • 힙 정렬
    • 특성
      • 힙 정렬은 이진 힙 자료구조를 사용하여 정렬을 수행하는 알고리즘이다.
      • 배열 내의 모든 요소를 힙으로 구성, 가장 큰 요소를 제거하고, 나머지 요소로 힙을 다시 구성하는 과정을 반복한다.
      • 이때 추가 메모리 사용이 거의 없고, 최악에도 시간복잡도 로그 스케일을 유지한다.
    • Best Case 시간복잡도 : O(NlogN)
    • Worst Case 시간복잡도 : O(NlogN)
  • 카운팅 정렬
    • 특성
      • 정렬할 요소의 범위가 제한적일때 사용하는 비교 기반 정렬 알고리즘이 아닌 방식이다.
      • 각 숫자의 출현 횟수를 계산하고, 이를 바탕으로 각 숫자의 위치를 배열에 직접 배치한다.
      • 정수나 일정 범위의 작은 숫자를 정렬할 때 매우 빠르고 효과적이다.
    • Best Case 시간복잡도 : O(n + k) k는 숫자 범위다.
    • Worst Case 시간복잡도 : O(n + k)
  • 기수 정렬
    • 특성
      • 각 자리수를 개별적으로 정렬하는 방식으로, 보통 최하위 자릿수부터 시작하여 최상위 자리수까지 차례로 정렬한다.
      • 카운팅 정렬과 같은 안정적인 정렬을 사용하여 각 자릿수를 정렬한다.
      • 기수 정렬은 숫자 범위가 클 때 카운팅 정렬 보단 효율적이다.
    • Best Case 시간복잡도 : O(n * k)
    • Worst Case 시간복잡도 : O(n * k)
  • 버킷 정렬
    • 특성
      • 여러 버킷(또는 버블)을 분배하고, 각 버킷을 개별적으로 정렬한 후, 결과를 하나로 병합하는 방식이다.
      • 데이터가 균등하게 분포된 경우 가장 잘 작동하고, 부동소수점 수를 정렬할 때 유용하다.
    • Best Case 시간복잡도 : O(N + K)
    • Worst Case 시간복잡도 : O(N^2)
      • 버킷 내의 요소가 균등하게 분배되지 않은 경우
  • LIS 알고리즘(Longest Increasing Subsequence)
    • 특성
      • 최장 증가 부분 수열을 발견하는 알고리즘이다
      • 이 수열은 연속적일 필요는 없으며, 순서만 유지하면 된다.
      • 동적 프로그래밍 방식 : 각 원소를 끝으로 하는 최장 증가 부분 수열의 길이를 찾는 방식
      • 이진 검색 방식 : 각 원소를 적절한 위치에 삽입하여 가장 긴 증가 부분 수열을 동적으로 구성한다.
      • LIS 자체는 부분을 구하는 공식이므로, 다른 알고리즘과 효과적으로 조합하면 배열을 위한 알고리즘 등으로 활용이 가능하다.
    • 동적 프로그래밍
      • Best Case : O(N^2)
      • Worst Case : O(N^2)
    • 이진 검색
      • Best Case : O(NlogN)
      • Worst Case : O(NlogN)
• 재귀에 대해 설명할 수 있다.
  • 우리가 아는 그 재귀, 일괄로 리턴값을 받는 그 재귀를 좀더 멋지게 표현하면 어떻게 표현하면 좋은가?
  • 재귀는 수학에서부터 빌려온 개념으로 반복되는 코드를 작성하기 보다 함수를 호출하는 방식으로 루프를 돌고, 목적이나 조건에 귀결되는 상황이 되었을 때 작업을 리턴하고 값을 반환하는 방식이다.
  • 재귀는 호출 될 때마다 스택프레임 구조가 호출되어, 함수 자신의 복사본이 메모리에 연거푸 구현된다.
  • 반복에 비해 코드가 단순해질 수 있으며, 무한 루프 발생 시 재귀의 경우 스택 오버플로우를 초래하여, 일정 면에서 종료 된다는 이점이 있다. 반복은 이에 비해 메모리에서 효율적이다보니 무한하게 반복에 들어가게 되는 경우, 인지하기 전까지 모르며, 시스템을 강제 종료 시키지 않으면안된다. 이러한 점 때문에 반복과 재귀는 알고리즘이나 특성을 고려하여 적절하게 사용하는게 중요하다.
• BFS/ DFS에 대해 설명할 수 있다. 직무 언어로 해당 알고리즘을 구현할 수 있다.
  • BFS(Breadth-First Search) :
    • 특성 BFS는 가장 가까운 노드부터 시작하여 점차 멀리 있는 노드를 탐색하며, 주변부를 완벽하게 확인, 이후 다음 깊이로 넘어가는 구조를 가진다.
    • 큐를 사용하여 구현하고, 각 노드를 방문 시 인접한 노드를 큐에 추가한다.
    • BFS 는 최단경로를 찾는 알고리즘에 사용되며 레밸별로 탐색이 되므로, 계층적 그래프 탐색에 적합하다.
    • 구현 예시

    import java.util.*;
    
    public class BFS {
    	private int V;
    	private LinkedList<Integer> adj[];
    	
    	public BFS(int v) {
    		this.V = v;
    		adj = new LinkedList[v];
    		for (int i = 0; i < this.V; ++i) {
    			adj[i] = new LinkedList();
    		}
    	}
    
    	void addEdge(int v, int w) {
    		adj[v].add(w); // 노드 v에 인접한 노드 w 추가
    	}
    
    	void BFS(int s) {
    		boolean visited[] = new boolean[this.V];
    		LinkedList<Integer> queue = new LinkedList<Integer>();
    
    		visited[s] = true;
    		queue.add(s);
    
    		while(queue.size() != 0) {
    			s = queue.poll(); // 원소 하나 제거하고 반환
    			System.out.print(s + " ");
    
    			Iterator<Integer> i = adj[s].listIterator();
    			while (i.hasNext()) {
    				int n = i.next();
    				if (!visited[n]) {
    					visited[n] = true;
    					queue.add(n)
    				}
    			}
    		}
    	}
    
    	public static void main(String args[]) {
            BFS g = new BFS(4);
    
            g.addEdge(0, 1);
            g.addEdge(0, 2);
            g.addEdge(1, 2);
            g.addEdge(2, 0);
            g.addEdge(2, 3);
            g.addEdge(3, 3);
    
            System.out.println("Breadth First Traversal (starting from vertex 2)");
    
            g.BFS(2);
        }
    }

  • DFS(Depth-First Search)
    • 우선적으로 노드의 깊이로 들어가서 탐색하는 구조로 탐색하는 알고리즘이다. 스택을 사용하거나 재귀 호출 등으로 구현이 가능하다.
    • 사이클 감지, 경로 탐색, 그래프의 후위 순회 등에 유용한 알고리즘이다.
    • 구현

    import java.util.*;
    
    public class DFS {
        private int V;   // 노드의 개수
        private LinkedList<Integer> adj[]; // 인접 리스트
    
        DFS(int v) {
            V = v;
            adj = new LinkedList[v];
            for (int i=0; i<v; ++i)
                adj[i] = new LinkedList();
        }
    
        void addEdge(int v, int w) {
            adj[v].add(w); // v에 인접한 노드 w 추가
        }
    
        void DFSUtil(int v, boolean visited[]) {
            visited[v] = true;
            System.out.print(v + " ");
    
            Iterator<Integer> i = adj[v].listIterator();
            while (i.hasNext()) {
                int n = i.next();
                if (!visited[n])
                    DFSUtil(n, visited);
            }
        }
    
        void DFS(int v) {
            boolean visited[] = new boolean[V];
            DFSUtil(v, visited);
        }
    
        public static void main(String args[]) {
            DFS g = new DFS(4);
    
            g.addEdge(0, 1);
            g.addEdge(0, 2);
            g.addEdge(1, 2);
            g.addEdge(2, 0);
            g.addEdge(2, 3);
            g.addEdge(3, 3);
    
            System.out.println("Depth First Traversal (starting from vertex 2)");
    
            g.DFS(2);
        }
    }
    

• 다익스트라, 프림, 플로이드-워셜, 벨만포드, 크루스칼 알고리즘 등 그래프에서 사용하는 알고리즘에 대해 알고 있는가?
  • 다익스트라 알고리즘
    • 목적 : 하나의 정점에서 다른 모든 정점까지의 최단 경로 탐색
    • 특성 : 가중치가 있는 그래프에서 사용되며, 음의 가중치르 가진 간선이 있을 경우 사용할 수 없다.
    • 방법 : 현재 정점에서 가장 가까운 정점을 우선적으로 선택하고 해당 정점에서 다른 정점으로의 거리를 갱신한다.
  • 프림 알고리즘
    • 목적 : 주어진 그래프의 최소 스패닝 트리(Minimum Spanning Tree)를 찾는다.
    • 특성 : 가중치가 있는 연결 그래프에서 사용되며, 크루스칼 알고리즘과 유사하다.
    • 방법 : 특정 정점에서 시작하여 선택된 정점 집합에 인접한 정점 중 최 가중치의 간선을 선택하여 트리를 확장한다.
  • 크루스칼 알고리즘(Kruskal’s Algorithm)
    • 목적 : 주어진 그래프의 MST 를 찾는다.
    • 특성 : 가중치가 있는 그래프에서 간섭을 가중치 순으로 정렬한 뒤, 순차적으로 선택하여 스패닝 트리를 구성한다.
    • 방법 : 유니온 파인드(Union-Find) 자료구조를 사용하고, 사이클이 형성되지 않는 선에서 간선을 추가한다.
  • 플루이드-워셜 알고리즘(Floyd-Warshall)
    • 목적 : 모든 쌍의 정점 간 최단 경로를 찾는다.
    • 특성 : 가중치 있는 그래프에서 음의 가중치가 있어도 사용 가능하다.
    • 방법 : 동적 프로그래밍 방식으로 각 정점 쌍 간의 최단 경로를 점진적으로 갱신한다.
  • 벨만-포드 알고리즘(Bellman-Ford)
    • 목적 : 하나의 정점에서 다른 모든 정점까지의 최단 경로를 찾으며, 음의 가중치가 있는 경우에도 사용이 가능하다.
    • 특성 : 음의 가중치가 있는 경로를 포함하여 음의 순환을 감지할 수 있다.
    • 방법 : 반복적으로 모든 간선을 검사하고, 최단 경로를 찾고, 음의 순환 존재 유무를 확인한다.
• 코드를 보고 시간 복잡도를 계산할 수 있다.
  • 코드의 시간 복잡도를 계산하는 것은 알고리즘의 성능에 대한 이해, 특정 입력 크기에 대해 얼마나 빨리 실행되는지 예측하는 데 중요한 역할을 한다.
  1. 코드의 기본 연산 이해하기 코드에서 가장 많이 일어날 영역을 파악한다. 반복문, 재귀 호출, 조건문 등 이러한 부분에서 실행시간이 가장 큰 영향을 준다.
  2. 반복문 문석 반복문이 얼마나 자주 일어나며, 그 대상의 범위가 어느정도 될지를 보면 된다. 복잡도는 배열 크기에 비례하여 해당 부분에서 O(N)이 된다.
  3. 중첩 반복문 확인 외부, 내부의 반복은 각각의 실행회수를 곱한 만큼 기본 연산이 수행되므로 O(NM)의 복잡도를 보여준다. 따라서 내외부가 동일한 경우 제곱이 되고, 중첩이 몇번 되냐에 따라 더 시간복잡도가 올라갈 수 있다.
  4. 재귀 함수 분석 각 호출에서 재귀가 호출되는 수준을 체크해야 하며 보통 O(NlogN) 내지는 O(logN) 정도의 복잡도를 추산할 수 있다.
  5. Worst, Average, Best 케이스 고려 알고리즘은 항상 최악-평균-최대 경우를 고려하여 시간복잡도를 판단해야 한다. 단 이때, 성능적인 지표는 최선 내지는 평균 보단 최악을 기준으로 고려하면 된다.
  6. 최대 차수를 확인하라 전체 코드의 양을 통해 시간 복잡도를 예상할 수 있게 되는데, 이때 일종의 방정식 형태가 된다. 그리고 거기서 대용량 처리에 가까운 입력을 받고, 반복문이 돌아간다고 하면 실질적으로 가장 높은 차수의 변수의 시간복잡도에 가깝고, 그 하위 변들은 실질적으로 의미가 없어진다(값의 크기 폭이 커서).

     O(N^3 + 4N + 15) 라는 시간복잡도가 있다고 할 때, 실질적으로 시간 복잡도는 O(N^3) 이다. 왜냐하면 N이 100을 기준으로 삼더라도 시간 복잡도는 O(1000000 + 400 + 15) 로 실질적으로 O(1000000)와 큰 차이가 없는 것이다.